See also
A Jupyter notebook version of this tutorial can be downloaded here.

[1]:
from copy import deepcopy
from typing import Callable
import matplotlib.pyplot as plt
import numpy as np
import rich # noqa:F401
from qcodes import ManualParameter
from scipy.optimize import least_squares
from scipy.signal import savgol_filter
from xarray.core.dataset import Dataset
import quantify_core.data.handling as dh
from qblox_instruments.simulations import exponential_overshoot_correction
from quantify_core.analysis.single_qubit_timedomain import SingleQubitTimedomainAnalysis
from quantify_core.visualization.mpl_plotting import (
set_suptitle_from_dataset,
set_xlabel,
set_ylabel,
)
from quantify_scheduler import QuantumDevice, Schedule, ScheduleGettable
from quantify_scheduler.backends.qblox import constants
from quantify_scheduler.backends.types.qblox import QbloxHardwareDistortionCorrection
from quantify_scheduler.device_under_test.quantum_device import DeviceElement
from quantify_scheduler.operations import (
X90,
Y90,
IdlePulse,
Measure,
Reset,
SquarePulse,
X,
)
from utils import ( # noqa:F401 # noqa:F401
display_dict,
initialize_hardware,
run_schedule,
show_connectivity,
)
[2]:
hw_config_path = "configs/tuning_transmon_coupled_pair_hardware_config.json"
device_path = "devices/transmon_device_2q.json"
[3]:
# Enter your own dataset directory here!
dh.set_datadir(dh.default_datadir())
Data will be saved in:
/root/quantify-data
[4]:
quantum_device = QuantumDevice.from_json_file(device_path)
qubit = quantum_device.get_element("q0")
quantum_device.hardware_config.load_from_json_file(hw_config_path)
cluster_ip = None
meas_ctrl, inst_coord, cluster = initialize_hardware(quantum_device, ip=cluster_ip)
Cryoscope#
This notebook replicates the Cryoscope protocol in this paper. Here’s the arxiv link.
Cryoscope is short for cryogenic oscilloscope, and is used to sample baseband pulses. This can then be used to correct the pulse distortions.
The experiment in this tutorial is meant to be executed with a Qblox Cluster controlling a flux-tunable transmon system.
The experiments can also be executed using a dummy Qblox device that is created via an instance of the Cluster class, and is initialized with a dummy configuration. However, when using a dummy device, simulated data will be generated and analyzed.
Hardware setup#
In this section we configure the hardware configuration which specifies the connectivity of our system.
Configuration file#
This is a template hardware configuration file for a single qubit system (we name the qubit q0), with a dedicated flux-control line.
The hardware setup is as follows, by cluster slot:
QCM-RF (Slot 6)
Drive line for
q0using fixed 80 MHz IF.
QCM (Slot 2)
Flux line for
q0.
QRM-RF (Slot 8)
Shared readout line for
q0using a fixed LO set at 7.5 GHz.
Note that in the hardware configuration below the mixers are uncorrected, but for high fidelity experiments this should also be done for all the modules.
Setup#
In this section we configure the hardware configuration which specifies the connectivity of our system.
The experiments of this tutorial are meant to be executed with a Qblox Cluster controlling a transmon system. The experiments can also be executed using a dummy Qblox device that is created via an instance of the Cluster class, and is initialized with a dummy configuration. When using a dummy device, the analysis will not work because the experiments will return np.nan values.
Configuration file#
This is a template hardware configuration file for a 2-qubit system with a flux-control line which can be used to tune the qubit frequency. We will only work with qubit 0.
The hardware connectivity is as follows, by cluster slot:
QCM (Slot 2)
\(\text{O}^{1}\): Flux line for
q0.\(\text{O}^{2}\): Flux line for
q1.
QCM-RF (Slot 6)
\(\text{O}^{1}\): Drive line for
q0using fixed 80 MHz IF.\(\text{O}^{2}\): Drive line for
q1using fixed 80 MHz IF.
QRM-RF (Slot 8)
\(\text{O}^{1}\) and \(\text{I}^{1}\): Shared readout line for
q0/q1using a fixed LO set at 7.5 GHz.
Note that in the hardware configuration below the mixers are uncorrected, but for high fidelity experiments this should also be done for all the modules.
Quantum device settings#
Here we initialize our QuantumDevice and our qubit parameters, checkout this tutorial for further details.
In short, a QuantumDevice contains device elements where we save our found parameters. Here we are loading a template for 2 qubits, but we will only use qubit 0.
Select the appropriate modules for this experiment:
A QCM baseband module for the flux line
A QCM-RF module for the XY drive line
A QRM-RF module for the readout
[5]:
cluster0 = cluster
Experiment setup#
Quantum device settings#
Here we use the quantum_device that has our qubit parameters, check out this tutorial for further details.
In short, a quantum_device contains device elements where we save our found parameters. If reinitialization is required, call quantum_device.close() to avoid restarting the kernel.
[6]:
q0 = quantum_device.get_element("q0")
q1 = quantum_device.get_element("q1")
Configure external flux control#
We need to have some way of controlling the external flux.
This can be done by setting an output bias on a QCM baseband module of the cluster which is then connected to the flux-control line.
Here we are nullifying the external flux on the qubit.
[7]:
# hardware_cfg["connectivity"]["graph"] contains a graph of how each physical output port
# connects to the device.
# Here we select the outputs that correspond to the flux, and then create a dict with
# a key:value pair `q*`:`cluster*.module*.out*_offset`
hardware_cfg = quantum_device.hardware_config()
flux_settables = {
element[1].split(":")[0]: eval(
".".join(element[0].split(".")[:2]) + f".out{element[0][-1]}_offset"
)
for element in hardware_cfg["connectivity"]["graph"]
if element[1][-3:] == ":fl"
}
for flux_settable in flux_settables.values():
flux_settable.inter_delay = 100e-9 # Delay time in seconds between consecutive set operations.
flux_settable.step = 0.3e-3 # Stepsize in V that this Parameter uses during set operation.
flux_settable() # get before set to avoid jumps
flux_settable(0.0)
Experiment#
As in the single qubit tuneup tutorial, the sweep setpoints for all experiments in this section are only examples. The sweep setpoints should be changed to match your own system. In this section we assume that each individual qubit has already been characterized, and that they have been biased to their sweetspots.
The Cryoscope method allows us to “capture” the flux pulse similar to an oscilloscope. It does this by first setting up two Ramsey-style experiments in which the gap between the two pi pulses is fixed: one where the second pi half pulse has the same phase, and another where the second pi half pulse is 90 degrees phase shifted. This allows us to measure the phase of the qubit on the equator of the Bloch sphere. In between the two pi half pulses, a flux pulse of small incremental duration is played in each iteration of the Ramsey style experiment, while the rest of the time between the pip half pulses is just idle time.
The flux pulse changes the qubit frequency while it is played, and the time integral of this frequency change gives the total phase accrued by the qubit. If we measure this cumulative phase for small incremental changes in the duration of the flux pulse, then we can effectively work out the frequency change in the qubit over time as the flux pulse is played by taking the derivative of the phase accrued vs time. Then using an already measured flux arc (qubit frequency vs flux), we can convert this frequency change over time to the actual flux seen by the qubit over time.
[8]:
def cryoscope_sched(
qubit: DeviceElement,
time_axis: np.ndarray,
x_or_y_axis: np.ndarray,
amplitude: float = 0.1,
start_pad: float = 40e-9,
end_pad: float = 100e-9,
repetitions: int = 1,
) -> Schedule:
"""
Generate a schedule for performing a Cryoscope experiment.
Parameters
----------
qubit
The name of the qubit e.g., :code:`"q0"` to perform the experiment on.
time_axis
The time axis for which the cryoscope experiment is run.
x_or_y_axis
Defines the pi half pulse after the wait time as an X90 or Y90.
amplitude
The amplitude of the flux pulse.
start_pad
The starting pad time of the flux pulse.
end_pad
The ending pad time of the flux pulse.
repetitions
The amount of times the Schedule will be repeated.
Returns
-------
:
An experiment schedule.
"""
schedule = Schedule("Cryoscope", repetitions)
# Calculate the additional time required to make
# one iteration take a multiple of 4 ns to complete.
idle_pulse_time = (
4e-9
- (
qubit.reset.duration()
+ start_pad
+ time_axis[-1] # Gap between pi half pulses excluding padding.
+ end_pad
+ 2 * qubit.rxy.duration()
+ qubit.measure.pulse_duration()
)
% 4e-9
)
# Create a dict x_or_y_op that assigns an X or Y gate to the binary keys
x_or_y_op = {0: X90(qubit.name), 1: Y90(qubit.name)}
# This IdlePulse is needed to have a starting point relative
# to which a relative time can be assigned to the Reset pulse.
schedule.add(IdlePulse(4e-9))
# Loop through the time axis. The last point is not used because
# it is used for the calibration points later.
for i, (time, x_or_y) in enumerate(zip(time_axis[:-2], x_or_y_axis[:-2])):
# Wait for additional time calculated above and then Reset the qubit.
schedule.add(Reset(qubit.name), label=f"Reset {i}", rel_time=idle_pulse_time)
# Move the qubit to the equator on the bloch sphere.
pi_half = schedule.add(X90(qubit.name))
if time > 0:
# Add the flux pulse of time t to the schedule
schedule.add(
SquarePulse(
amp=amplitude, duration=time, port=qubit.ports.flux(), clock="cl0.baseband"
),
ref_op=pi_half,
rel_time=start_pad,
)
# Wait for the gap time and play the second pi half pulse.
# This pi half pulse is either an X90 or Y90.
schedule.add(
x_or_y_op[x_or_y], ref_op=pi_half, rel_time=start_pad + time_axis[-1] + end_pad
)
# Measure the qubit.
schedule.add(Measure(qubit.name, acq_index=i), label=f"Measurement {i}")
# Calibration points measured by preparing ground and excited states.
schedule.add(Reset(qubit.name), label="Reset Cal 0")
schedule.add(Measure(qubit.name, acq_index=i + 1), label="Calibration 0")
schedule.add(Reset(qubit.name), label="Reset Cal 1")
schedule.add(X(qubit.name))
schedule.add(Measure(qubit.name, acq_index=i + 2), label="Calibration 1")
return schedule
Create a CryoscopeAnalysis class#
This class extends the class SingleQubitTimedomainAnalysis from quantify_core.analysis.single_qubit_timedomain:
Specify that the
run()method uses calibration pointsExtend the
process_data()method to populateself.dataset_processedwith anxarraydataset:coords:
"Time (ns)"axis:
"frequency_change"axis:
"reconstructed_phi"
Add method
create_figures()
[9]:
class CryoscopeAnalysis(SingleQubitTimedomainAnalysis):
"""
Analysis class for the Cryoscope experiment.
This class extends the SingleQubitTimedomainAnalysis class, which in turn extends the
BaseAnalysis class:
- BaseAnalysis.run() runs all steps in the AnalysisSteps class:
1. process_data # Empty
2. run_fitting # Empty
3. analyze_fit_results # Empty
4. create_figures # Empty
5. adjust_figures # Defined
6. save_figures # Defined
7. save_quantities_of_interest # Defined
8. save_processed_dataset # Defined
9. save_fit_results # Defined
- SingleQubitTimedomainAnalysis extends BaseAnalysis:
- run() defines self.calibration_points
- process_data() populates dataset_processed.S21 and dataset_processed.pop_exc
- CryoscopeAnalysis extends SingleQubitTimedomainAnalysis:
- process_data() is extended by calculating:
- x_vals, y_vals
- unfiltered_phase
- filtered_phase
- unwrapped_phase
- phase_derivative
- frequency_change
- reconstructed_phi
- create_figures() is defined
"""
def __init__( # noqa: D107
self,
dataset: Dataset = None,
tuid: str = None,
label: str = "",
settings_overwrite: dict = None,
plot_figures: bool = True,
frequency_change_to_flux: Callable = None,
savgol_filter_params: dict = {"window_length": 2, "polyorder": 1},
) -> None:
super().__init__(dataset, tuid, label, settings_overwrite, plot_figures)
self.frequency_change_to_flux = frequency_change_to_flux
self.savgol_filter_params = savgol_filter_params
def run(self):
"""
Run the SingleQubitTimedomainAnalysis with calibration_points.
This removes the calibration points (last two) and converts
the rest of the IQ values to a population (pop_exc).
"""
return super().run(calibration_points=True)
def process_data(self) -> None: # noqa: D102
super().process_data()
# Translate and scale the populations from X and Y measurements
# from the range [0,1] to [-1,1]
x_vals = 2 * (self.dataset_processed["pop_exc"].values[:-2:2] - 0.5)
y_vals = 2 * (self.dataset_processed["pop_exc"].values[1:-2:2] - 0.5)
# Find phase from the X,Y coordinates
unfiltered_phase = np.angle(x_vals + 1j * y_vals)
# Store the unfiltered phase for debugging purposes
self.dataset_processed["unfiltered_phase"] = (["t"], unfiltered_phase)
# First unwrap the phase
unwrapped_phase = np.unwrap(unfiltered_phase)
# Store the unwrapped phase for debugging purposes
self.dataset_processed["unwrapped_phase"] = (["t"], unwrapped_phase)
# Use the savgol_filter to both filter and take the derivative of the unwrapped phase.
# The parameters of the savgol_filter may need to be changed after this is run on an
# actual device.
filtered_phase_derivative = savgol_filter(
unwrapped_phase,
window_length=self.savgol_filter_params["window_length"],
polyorder=self.savgol_filter_params["polyorder"],
deriv=1,
)
# Store the filtered phase derivative for debugging purposes
self.dataset_processed["filtered_phase_derivative"] = (["t"], filtered_phase_derivative)
# Rescale the filtered phase derivative to units of frequency change
frequency_change = filtered_phase_derivative / (
self.dataset_processed.x1[2].values - self.dataset_processed.x1[0].values
)
# Store the frequency change
self.dataset_processed["frequency_change"] = (["t"], frequency_change)
# if frequency_change_to_flux is provided, convert the frequency to flux (reconstructed_phi) and plot this.
if self.frequency_change_to_flux is not None:
reconstructed_phi = self.frequency_change_to_flux(frequency_change)
self.dataset_processed["reconstructed_phi"] = (["t"], reconstructed_phi)
else:
print(
"frequency_change_to_flux was not provided, reconstructed_phi has not been calculated."
)
def create_figures(self) -> None: # noqa: D102
fig, ax = plt.subplots()
fig_id = "Cryoscope"
self.figs_mpl[fig_id] = fig
self.axs_mpl[fig_id] = ax
# if frequency_change_to_flux is provided, plot it.
if self.frequency_change_to_flux is not None:
ax.plot(
1e9 * self.dataset_processed["reconstructed_phi"].coords["t"],
self.dataset_processed["reconstructed_phi"],
label="Measured",
)
set_ylabel(r"Reconstructed $\Phi/\Phi_0$")
# if frequency_change_to_flux is not provided, plot the frequency change.
else:
ax.plot(
1e9 * self.dataset_processed["frequency_change"].coords["t"],
self.dataset_processed["frequency_change"] / 1e6,
label="Measured",
)
set_ylabel("Frequency change (MHz)")
set_xlabel("Time (ns)")
set_suptitle_from_dataset(fig, self.dataset)
Define the flux dependence of the qubit frequency#
This is qubit specific, and assumes that the qubit has already been characterized. In the simplest case of a symmetric qubit (i.e. one with identical JJs in the SQUID), only \(E_\text{J}\) and \(E_\text{C}\) need to be provided.
[10]:
def flux_to_frequency_change(flux: np.ndarray):
"""
Convert frequency to flux.
Currently this assumes a symmetric qubit and fixed parameters.
Args:
----
flux (np.ndarray): an array of flux values, in units of flux quantum
"""
h = 1 / (2 * np.pi)
e_c = h * 300e6
e_j = (h * q0.clock_freqs.f01() + e_c) ** 2 / (8 * e_c)
return (1 / h) * (
np.sqrt(8 * e_j * e_c * np.abs(np.cos(np.pi * flux))) - e_c
) - q0.clock_freqs.f01()
def frequency_change_to_flux(freq_change: np.ndarray):
r"""
Convert flux to frequency.
\Phi(\tau) = \pm \Phi_0/\pi \arccos((Ec+h*freq_change)**2/(8*Ej*Ec)),
or in units of flux quantum:
|\Phi(\tau)/\Phi_0| = arccos((Ec+h*freq_change)**2/(8*Ej*Ec))/pi.
"""
# Assuming the qubit is parked at the maximum frequency, we can clip positive frequency changes to zero
freq_change = np.clip(freq_change, None, 0)
h = 1 / (2 * np.pi)
e_c = h * 300e6
e_j = (h * q0.clock_freqs.f01() + e_c) ** 2 / (8 * e_c)
return (
np.arccos((h * (q0.clock_freqs.f01() + freq_change) + e_c) ** 2 / (8 * e_j * e_c)) / np.pi
)
Define the shape of the flux pulse#
When testing with a dummy cluster, this should mimic the distortions of the cables.
When running on a real device, this should be a true step function.
[11]:
def flux_pulse_shape(t: np.ndarray):
"""
Shape of the flux pulse send to the qubit.
Predistortion calculated using the Qblox simulator for the exponential overshoot correction
using values in the cluster to simulate the real time predistortions,
and an exponential overshoot distortion is added to the signal
that is fixed to simulate a real distortion.
"""
signal = 0.1 * (1 + 0.05 * np.exp(-t / 72e-9))
signal[np.where(t <= 0)] = 0.0
return exponential_overshoot_correction(
signal,
cluster0.module2.out0_exp0_amplitude(),
max(cluster0.module2.out0_exp0_time_constant(), 6),
)
Define simulated data when running on a dummy cluster#
[12]:
def get_simulated_cryoscope_data():
"""Convert the flux pulse shape to cryoscope data."""
# Convert the flux pulse shape to frequency change.
freq_change = flux_to_frequency_change(flux_pulse_shape(time_axis()[::2]))
freq_change -= freq_change[0]
cumulative_phase_change = np.cumsum(2 * np.pi * freq_change) * np.diff(time_axis()[:4:2])[0]
# Define IQ values for ground state and excited state
ground_state = 0
excited_state = 1 + 5.0j
# compute the IQ values for the X measurements
x_measurements = (np.cos(cumulative_phase_change) * 0.5 + 0.5) * excited_state
# compute the IQ values for the Y measurements
y_measurements = (np.sin(cumulative_phase_change) * 0.5 + 0.5) * excited_state
# Assign the last of the x and y measurements
# to ground and excited state IQ values
x_measurements[-1] = ground_state
y_measurements[-1] = excited_state
# reshape to the way that an actual measurement would look like
result = np.concatenate((x_measurements, y_measurements)).reshape(2, -1).T.flatten()
return [np.real(result), np.imag(result)]
def simulated_get():
"""Run the previous get function but only return simulated data."""
gettable.old_get()
return get_simulated_cryoscope_data()
Define the schedule gettables for the measurement#
[13]:
time_axis = ManualParameter(name="time_axis", unit="(ns)", label="Time")
time_axis.batched = True
x_or_y = ManualParameter(name="x_or_y", unit="", label="axis")
x_or_y.batched = True
cryoscope_kwargs = {
"time_axis": time_axis,
"x_or_y_axis": x_or_y,
"amplitude": 0.156,
"qubit": quantum_device.get_element("q0"),
}
gettable = ScheduleGettable(
quantum_device,
schedule_function=cryoscope_sched,
schedule_kwargs=cryoscope_kwargs,
real_imag=True,
batched=True,
)
# replace the get method for the gettable in case the cluster is a dummy
if cluster_ip is None:
gettable.old_get = gettable.get
gettable.get = simulated_get
# Set the number of repetitions (or averages)
quantum_device.cfg_sched_repetitions(1)
Define the time spacing between pulses#
This allows for transients to decay.
[14]:
constants.PULSE_STITCHING_DURATION = 16e-9
Measure the phase vs the duration of the detuning flux pulse#
[15]:
time_axis_setpoints = np.arange(-5e-9, 200e-9, 1e-9)
x_or_y_setpoints = [0, 1]
meas_ctrl.settables([x_or_y, time_axis])
meas_ctrl.setpoints_grid([x_or_y_setpoints, time_axis_setpoints])
# Pass the ScheduleGettable class with schedule_function=cryoscope_sched on to the measurement control
meas_ctrl.gettables(gettable)
hw_cfg = quantum_device.hardware_config()
[16]:
if hw_cfg.get("hardware_options", {}).get("distortion_corrections") is not None:
# In case the cells below have already been run, we need to reset the distortion_corrections hardware option again.
print(
f"Predistortion filter removed. Previous value: {hw_cfg['hardware_options'].pop('distortion_corrections', None)}"
)
# Run the measurement control loop
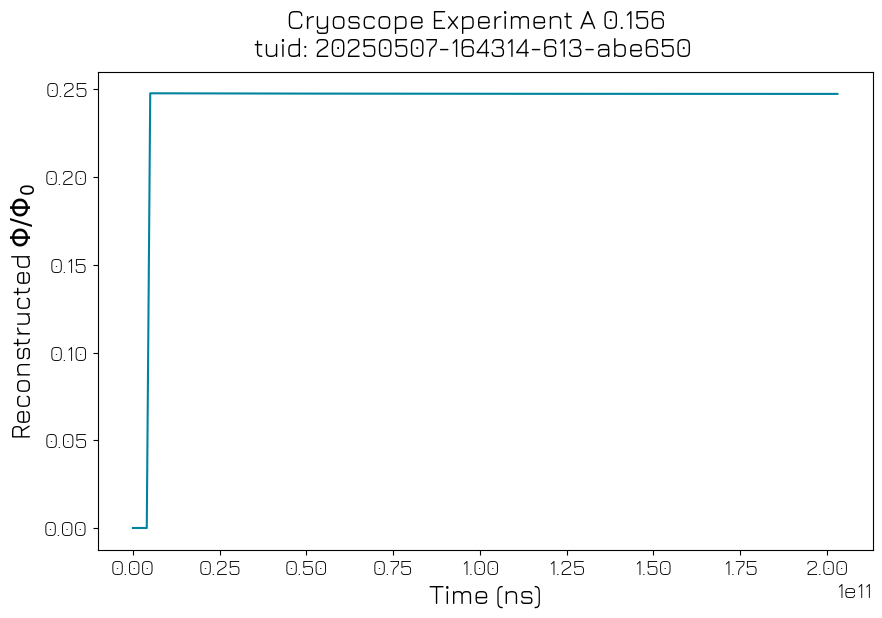
cryoscope_ds = meas_ctrl.run(f"Cryoscope Experiment A {cryoscope_kwargs['amplitude']}")
# Analyze the date from the measurement
if cluster_ip is None:
savgol_filter_params = {"window_length": 2, "polyorder": 1}
else:
savgol_filter_params = {"window_length": 10, "polyorder": 1}
cryoscope_result = CryoscopeAnalysis(
dataset=cryoscope_ds,
label="Cryoscope",
settings_overwrite={"mpl_transparent_background": False},
frequency_change_to_flux=frequency_change_to_flux,
savgol_filter_params=savgol_filter_params,
).run()
cryoscope_result.display_figs_mpl()
Starting batched measurement...
Iterative settable(s) [outer loop(s)]:
--- (None) ---
Batched settable(s):
x_or_y, time_axis
Batch size limit: 410
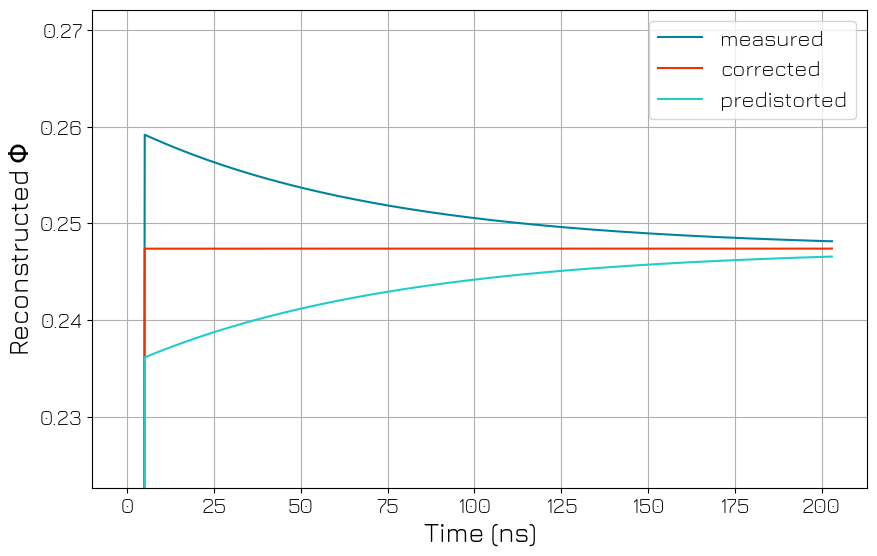
Calculate the predistortion needed to send a square pulse#
In order to find the optimal parameters for the overshoot correction, we define the residual as the difference between exponential_overshoot_correction() applied to the measured \(\Phi/\Phi_0\), and the ideal pulse shape.
[17]:
# Define the residual for the fitting function
def residual(params: list, distorted_data: np.ndarray):
# Params are [amp,tau,scale]
distorted_data = deepcopy(distorted_data.values)
# Remove the offset: subtract the value of the first data point from the data array
distorted_data -= distorted_data[0]
# Scale the data by scaling parameter
distorted_data /= 2 * params[2]
# Define the ideal pulse as a step function with height 0.5 starting at t=0
ideal = 0.5 * np.ones(len(distorted_data))
ideal[:5] = 0
return exponential_overshoot_correction(distorted_data, params[0], params[1]) - ideal
Find a best fit for the predistortion filter that would result in a clean pulse at the qubit using the least squares method.
[18]:
time = cryoscope_result.dataset_processed.t
# Convert xarray.DataArray to np.array, store the results separately in memory
distorted_data = cryoscope_result.dataset_processed.reconstructed_phi
# Find the overshoot correction parameters that best approximate the ideal pulse shape
res = least_squares(residual, x0=(0.33, 73, 0.1), args=(distorted_data,))
/builds/0/.venv/lib/python3.9/site-packages/qblox_instruments/simulations/predistortions.py:77: UserWarning: Qblox simulator plugin WARNING: Output will be clipped.The result of the simulation cannot be trusted.
warnings.warn(
Plot the measured pulse shape versus the corrected and predistorted pulse shapes
[19]:
ideal = res.x[2] * np.ones(len(distorted_data))
ideal[:5] = 0
fig, ax = plt.subplots()
ax.plot(time, distorted_data, label="measured")
ax.plot(
time, exponential_overshoot_correction(distorted_data, res.x[0], res.x[1]), label="corrected"
)
ax.plot(time, exponential_overshoot_correction(ideal, res.x[0], res.x[1]), label="predistorted")
if cluster_ip is None:
ax.set_ylim(0.9 * res.x[2], 1.1 * res.x[2])
ax.set_xlabel("Time (ns)")
ax.set_ylabel(r"Reconstructed $\Phi$")
ax.legend()
ax.grid()
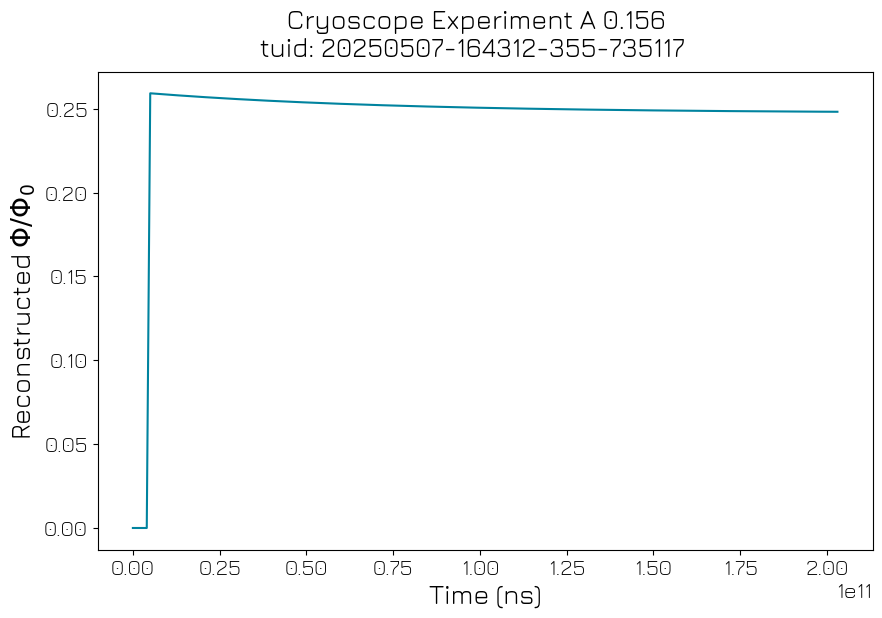
Repeat the measurement of the phase vs the duration of the detuning flux pulse#
This time with the predistortion filter applied.
[20]:
# Set the hardware distortions for the relevant flux line.
hw_cfg["hardware_options"]["distortion_corrections"] = {
"q0:fl-cl0.baseband": QbloxHardwareDistortionCorrection(exp0_coeffs=[res.x[1], res.x[0]])
}
quantum_device.hardware_config(hw_cfg)
cryoscope_ds = meas_ctrl.run(f"Cryoscope Experiment A {cryoscope_kwargs['amplitude']}")
cryoscope_result = CryoscopeAnalysis(
dataset=cryoscope_ds,
label="Cryoscope",
settings_overwrite={"mpl_transparent_background": False},
frequency_change_to_flux=frequency_change_to_flux,
).run()
cryoscope_result.display_figs_mpl()
Starting batched measurement...
Iterative settable(s) [outer loop(s)]:
--- (None) ---
Batched settable(s):
x_or_y, time_axis
Batch size limit: 410